| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 프로토콜 #네트워크 #통신 #컴퓨터
- 데이터베이스 #제약조건
- chatgpt # chatgpt api
- 딥러닝 #퍼셉트론 #perceptron #신경망 #neural network
- 기하와 벡터 #직선 #직선의 방정식 #벡터 #방향벡터
- 해석학 #유계 #상계 #하계 #집합
- 일차종속 #일차독립 #선형대수학 #벡터공간
- subspace #부분공간 #선형대수학
- 삼각함수 #sin #cos #tan
- 유클리드 기하학 #유클리드 공준 #기하학 #중등 기하 #평면 기하
- 완비성공리 #실수
- C# #unity #유니티
- OSI #OSI 7계층 #컴퓨터 네트워크
- 리액트 #React #컴포넌트 #component
- 수학 #공리 #정의 #정리 #명제
- 실수 #성질 #정리 #체 #Field #공리
- chatGPT #openAI #인공지능 #chatGPT4
- React #Hooks
- 라디안 #호도법 #각도 #기하 #고등수학 #수학
- span #generate
- C# #Framework #.NET
- React #리액트 #component #life cycle
- 아르키메데스 #Archimedean Property #해석학 #Analysis
- Database #DBMS
- 해석학 #상한 #하한 #최댓값 #최솟값
- AI #math #function
- 선형대수학 #벡터공간 #벡터 #수학
- 데이터베이스 #키 #key #슈퍼키 #super key #외래키 #foreign key #후보키 #candidate key #기본키 #primary key
- raspberrypi #라즈베리파이4 #ssh
- chatgpt api
- Today
- Total
기록하고 기록하면 어떻게 될까
[해석학] 상한 supremum, 하한 infimum 에 대해 알아보자 본문
지난번 글을 통해 유계와 관련된 용어들을 다뤘다. 이번 글은 그 때 다룬 상계 upper bound와 하계 lower bound 개념의 연장선상에 있는 상한 supremum 과 하한 infimum 에 대해 다뤄보겠다.
사실 상계 upper bound 와 하계 lower bound 의 정의를 잘 이해한다면 상한과 하한은 그냥 따라 오는 개념이라 생각할 수 있다.
상한 supremum 그리고 하한 infimum 의 정의
공집합이 아닌 실수 집합 $\mathbb{R}$ 의 부분집합 $S$를 생각하자.
- 상한 Supremum
집합 $S$가 위로 유계이면, 집합 $S$의 상한 $u$는 다음 두 조건들을 만족하며 $Sup \; S$ 로 표기한다.
If $S$ is bounded above, then a number $u$ is said to be a supremum(=least upper bound) of $S$ if it satisfies the conditions. $\Leftrightarrow$ $Sup$ $S$
1. $u$는 집합 $S$의 상계 upper bound 이다. $u$ is an upper bound of $S$
2. 만약 $v$가 집합 $S$의 또 다른 상계라면 $u \le v$ 이다. If $v$ is any upper bound of $S$, then $u≤v$
(2') For every $\epsilon > 0$, there exists $s \in S \; s.t . \; u - \epsilon < s \le u $
- 하한 Infimum
집합 $S$가 아래로 유계이면, 집합 $S$의 하한 $w$는 다음 두 조건들을 만족하며 $Inf \; S$ 로 표기한다.
If $S$ is bounded below, then a number $w$ is said to be an infimum(=greatest lower bound) of $S$ if it satisfies the conditions. $\Leftrightarrow$ $Inf$ $S$
- $w$는 집합 $S$의 하계 lower bound 이다. $w$ is a lower bound of $S$
2. 만약 $t$가 집합 $S$의 또 다른 하계라면 $t \le w$이다. If $t$ is any lower bound of $S$, then $t ≤ w$
(2') For every $\epsilon > 0$, there exists $s \in S \; s.t . \; w \le s < w + \epsilon $
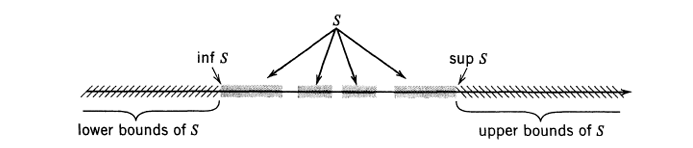
그러면 이제는 우리가 잘 안다고 생각하는 개념인 최댓값과 최솟값에 대해 살펴보고 상한,하한과 비교를 해보자 .
우선 최댓값, 최솟값부터 살펴보자
최댓값 Maximum과 최솟값 Minimum의 정의
공집합이 아닌 실수 집합 $\mathbb{R}$ 의 부분집합 $S$를 생각하자.
최댓값 Maximum
$a_0$가 집합 $S$의 원소라고 하자. 이 때 $\forall$$a$ $\in$ $S$ , $a$$_0$ $≥ a$ 이면 $a_0$를 집합 $S$의 최댓값 이라 한다.
Let $a$$_0$ $\in $ $\mathbb{R} $ is an element of set $S$. If $\forall$$a$ $\in$ $S$ , $a$$_0$ $≥ a$, then $a$$_0$ is called $maximum$ of set $S$
최솟값 Minimum
$a_1$가 집합 $S$의 원소라고 하자. 이 때 $\forall$$a$ $\in$ $S$ , $a$$_1$ $\le a$ 이면 $a_1$를 집합 $S$의 최솟값 이라 한다.
Let $a$$_1$ $\in$ $\mathbb{R} $ is an element of set $S$. If $\forall$$a$ $\in$ $S$ , $a$$_1$ $≤ a$, then $a$$_1$ is called $minimum$ of set $S$
그렇다면 상한,하한과 최대,최솟값의 차이점은 무엇인가?
이는 해당 값이 집합에 속하는지 유무에 있다.
최댓값과 최솟값의 정의를 보면 그 값이 우선 해당 집합 $S$ 의 원소여야 한다. 하지만 상한과 하한은 해당 집합 $S$ 의 원소여야 한다는 조건이 없다. 따라서 이 용어들은 비슷하지만 차이점을 가진다.
'Analysis > Real Analysis' 카테고리의 다른 글
| [해석학] 아르키메데스 성질 Archimedean Property (0) | 2023.03.20 |
|---|---|
| [해석학] 완비성 공리 The completeness Axiom of Real Numbers (0) | 2023.03.16 |
| [해석학] 유계 bounded, 상계 upper bound, 하계 lower bound 에 대해서 (0) | 2023.02.22 |



